Page updated:
October 13, 2021
Author: Curtis Mobley
View PDF
Radiative Transfer Equations
This chapter discusses light from the viewpoint of radiative transfer theory. The Theory of Electromagnetism chapter discusses light from the viewpoint of the classical theory of electromagnetism, i.e., using Maxwell’s equations.
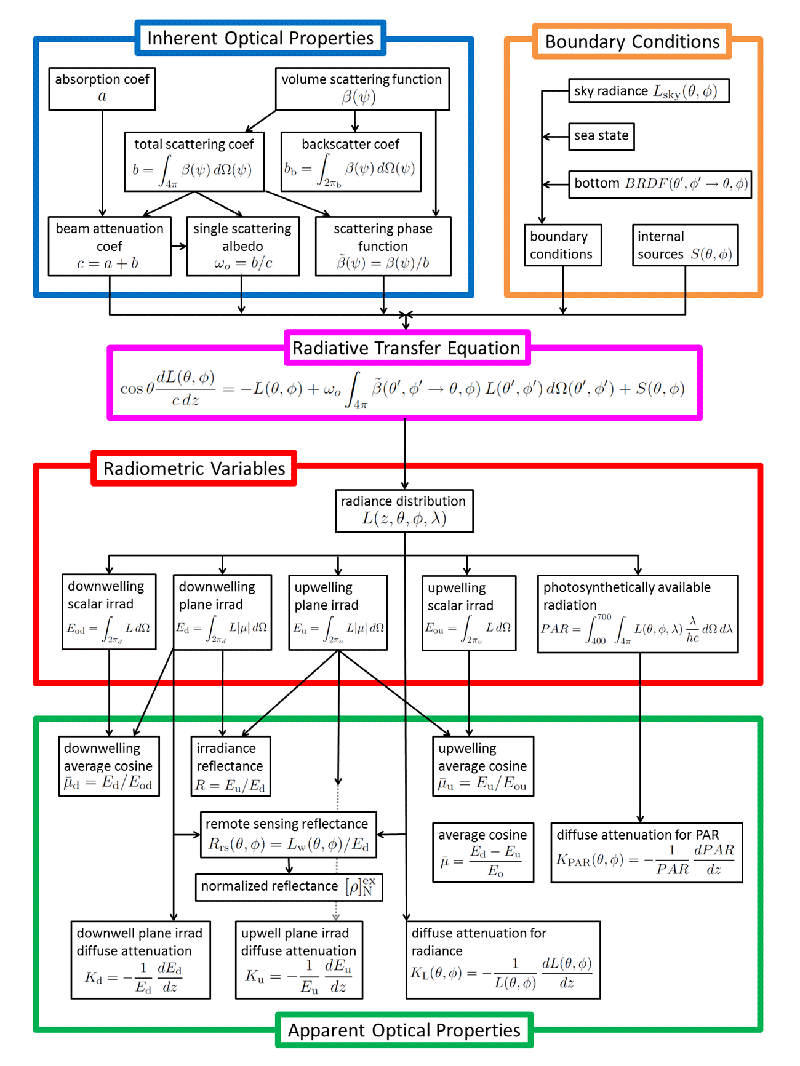
The Light and Radiometry chapter showed how various physical and mathematical quantities such as energy and solid angle can be combined to describe light in terms of radiance. The Inherent and Apparent Optical Properties chapter showed how various inherent optical properties (IOPs) are used to describe the optical properties of the medium through which light propagates. This chapter now develops the radiative transfer equations that tie together those two sets of properties and thereby provide the theoretical framework for all of optical oceanography and ocean-color remote sensing. The“organization chart” seen in Figure 1 shows the central role of radiative transfer theory and the radiative transfer equation. In essence, IOPs and boundary conditions go into the equation, radiance comes out, and all irradiances and apparent optical properties (AOPs) are then computed from the radiance.
The radiative transfer equation shown in the purple box of Fig. 1 is the scalar (ignoring polarization) radiative transfer equation (SRTE). It is derived in a qualitative fashion on the SRTE Heuristic Development page.
There is actually a hierarchy of radiative transfer equations (RTEs). At the top is a very general equation (Eq. 2 of the The General Vector Radiative Transfer Equation page) capable of describing polarized light propagation in matter that is directionally non-isotropic, that can absorb light differently for different states of polarization, and that contains scattering particles of any shape and random or non-random orientation. Although very general in its ability to simulate any situation encountered in optical oceanography, the full set of IOP inputs to this equation is never measured in the oceanographic setting.
The IOP inputs to the most general equation become considerably simpler if the medium has mirror symmetry, as explained on the The VRTE for Mirror-symmetric Media page. The resulting equation is suitable for computation of polarized radiative transfer in the oceanic setting, especially after restriction to a plane-parallel geometry (Eq. 3 of that page).
The vector-level equations can be further simplified as shown on the The Scalar Radiative Transfer Equation page to obtain, in a rigorous fashion, the equation shown in Fig. 1. That equation for the total radiance is only approximate, but the inputs are simple enough to measure and model, so this equation finds wide use in oceanography.
These vector and scalar RTEs are derived on the Level 2 pages referenced above.
The radiance-level RTEs yield further equations involving the irradiances. One example is the two-flow equations for the plane irradiances and seen in Light and Water Section 5.11. However, those equations cannot be solved for the irradiances unless ad hoc assumptions are made about the angular shape of the radiance distribution. Although once important, the two-flow equations have little value now that computers allow for very accurate numerical solutions of both the vector and scalar radiative transfer equations. The two-flow equations are therefore not discussed here.
Solution of the vector and scalar RTEs must be done numerically except for a few trivial cases such as non-scattering media. Approximate analytical solutions for the radiance can be obtained under very restrictive (and unphysical) conditions such as a sun in a black sky and only single scattering within the water. These single-scattering solutions are developed on pages The Single-Scattering Approximation and The Quasi-Single-Scattering Approximation.
There are also irradiance-level ”solutions” of the scalar RTE such as Gershun’s Law.
Because of the mathematical nature of radiative transfer theory, most of the material for this chapter is in the Level 2 pages.

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.