Page updated:
May 19, 2021
Author: Curtis Mobley
View PDF
Normalized Reflectances
[Howard Gordon and David Antoine also contributed to this page.]
Ocean-color remote sensing algorithms usually work with remote-sensing reflectances or normalized water-leaving reflectances. The calculation and interpretation of those quantities are discussed in detail on this page.
The ratio of water-leaving radiance to incident sky irradiance is an apparent optical property (AOP) that has only weak dependence on external parameters such as solar zenith angle and sky conditions, but which is strongly correlated with water-column inherent optical properties (IOPs). However, the remote-sensing reflectance still does depend somewhat on the atmospheric and other conditions at the time of measurement and thus, strictly speaking, is tied to the particular time and location of the observation. (Further discussion and examples are given on the Reflectances page.)
It would be desirable to have an AOP that completely removes the effects of solar zenith angle, viewing direction, atmospheric conditions, and sea state, while retaining a strong dependence on the water IOPs. It would then be possible to compare this AOP for measurements made at different times and/or locations, and thereby extract information about the differences in the water columns for the different measurements. Even for measurements made at the same time and location, normalization to a common set of conditions is needed, e.g., when comparing in situ measurements having different viewing directions. Such an AOP is obtained via the concept of the normalized water-leaving reflectance.
Normalized Radiances and Reflectances
Let be the in-water, upwelling radiance at depth , for a Sun zenith angle of and a viewing direction of . Polar viewing direction indicates a direction looking at the nadir, detecting radiance traveling toward the zenith. The azimuthal angle is measured relative to the Sun’s azimuthal direction. denotes the corresponding water-leaving radiance, which is measured just above the sea surface. These radiances depend strongly on wavelength, which is not shown. In practice, is measured by instruments in the water. can be obtained by atmospheric correction of a radiance measured at the top of the atmosphere, from an above-surface measurement at sea level after correction for surface reflectance, or from an in-water measurement of extrapolated upward through the sea surface.
One goal of normalization is to transform a satellite-based measurement of top-of-the-atmosphere radiance into something that can be compared with a standard measurement made in situ, in the ocean, for whatever Sun zenith angle, viewing direction, atmospheric conditions, and wave state occurred at the time of the satellite measurement. Let this standard in situ measurement be the nadir-viewing radiance measured just below the sea surface, . Depth refers to a location in the water just below the sea surface; refers to a location in the air just above the sea surface. Dividing by the downwelling plane irradiance within the water, , gives the in-water Remote Sensing Ratio :
| (1) |
The division of by removes the “zeroth order” effect of solar zenith angle and the “first order” atmospheric effects (including aerosol effects) on the magnitude of . We now want to transform into something comparable.
In the early days of satellite remote sensing, it was sometimes assumed that the upwelling underwater radiance distribution is isotropic. Under that assumption, is approximately what you would get if the Sun were at the zenith and there were no atmosphere (i.e., the sky were black). This was the origin of statements that the normalized water-leaving radiance is the water-leaving radiance ”which would exit the sea surface if the Sun were at the zenith and if the atmosphere were absent” (Gordon et al. (1988), page 10,910).
Fig. 1 compares upwelling and water-leaving radiances for “no atmosphere” or “black sky” vs. realistic sky conditions. The curves of this figure were generated using HydroLight with the Sun placed at the zenith. The sky was either black (a collimated incident sky radiance) or had a diffuse radiance angular distribution typical of a clear sky. The water IOPs were determined using the same “new Case 1” bio-optical model as for the simulations of the previous page. Runs were made for chlorophyll values of 0.05, 0.5 and 5 . The runs were at a wavelength of 550 nm and the sea surface was level. Each radiance is normalized by its value at the nadir-viewing direction to isolate the differences in the shapes of the curves. The upper set of curves shows the shape of the upwelling radiances just below the sea surface as functions of the in-water, off-nadir viewing angle at right angles () to the solar plane. The lower set of curves (those curving downward in the figure) shows the corresponding water-leaving radiances as functions of the in-air, off-nadir viewing angle . For a level sea surface, these in-water and in-air angles are related by Snel’s law , where is the water index of refraction. Although the differences in the black-sky and real-sky radiances are only a few percent over the range of angles relevant to most remote sensing ( deg), differences of this magnitude are significant given the high accuracy requirements for retrieved water-leaving radiances in ocean remote sensing.
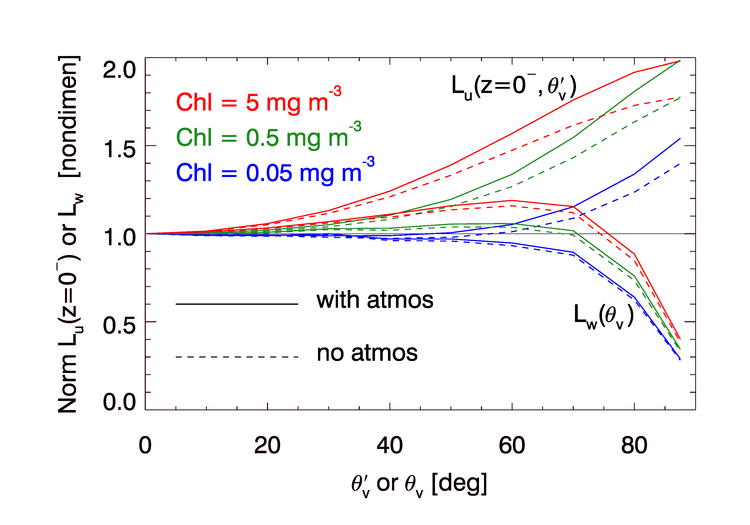
The observation that the upwelling radiance distribution depends on the sky radiance distribution indicates that the idea of removing the atmosphere is too extreme.Morel and Gentili (1996) (page 4852) therefore revised the definition of normalized water-leaving radiance to be “...the radiance that could be measured by a nadir-viewing instrument, if the Sun were at the zenith in the absence of any atmospheric loss, and when the Earth is at its mean distance from the Sun.” The distinction between “atmosphere were absent” (i.e., a vacuum) and “absence of any atmospheric loss” (i.e., no attenuation by the atmosphere) is fundamental to understanding the developments of this section.
The normalization proceeds as follows. The first step is to account for solar zenith angle and atmospheric attenuation effects on via (e.g., Gordon and Clark (1981), page 10,910; or Gordon and Wang (1994b), Eq. 4):
where is the atmospheric diffuse transmittance for irradiance in the Sun’s direction for the given atmospheric conditions. Recent papers include an explicit factor to correct for the Earth-Sun distance at the time of measurement:
| (2) |
Here is the Earth-Sun distance at the time of measurement, and is the mean Earth-Sun distance. The factor corrects the measurement to what it would be at the mean Earth-Sun distance. (The solar irradiance at the TOA varies by about 8% over the course of a year due to the Earth’s elliptical orbit.)
is called the normalized water-leaving radiance. It is the water-leaving radiance that would occur if the earth were at the mean Earth-Sun distance, the Sun were at the zenith, and the atmosphere were non-attenuating. Note that although the factors of , , and largely remove the effects of Earth-Sun distance, solar zenith angle, and atmospheric attenuation, respectively, on the measured , the normalized water-leaving radiance still refers to a particular viewing direction and depends on the sky angular radiance distribution at the time of observation.
Multiplying the of Eq. (2) by a factor of , where has units of steradian and is the extraterrestrial solar irradiance at the mean Earth-Sun distance, gives the nondimensional normalized water-leaving reflectance (Gordon and Wang (1994b), page 7756):
| (3) |
(Radiant energy is a physical quantity that propagates through space and that can leave the water. Radiance is a derived physical quantity that likewise can leave the water, so it makes sense to speak of the “water-leaving radiance.” Reflectance, however, is a property of a surface. Reflectance does not propagate through space and it cannot leave a surface, so it does not make sense to speak of the “water-leaving reflectance.” However, the term “water-leaving reflectance” is well established shorthand for “reflectance based on the water-leaving radiance and the incident irradiance,” and we will use the term even if it is linguistically somewhat improper.)
The remote-sensing reflectance is usually defined as
| (4) |
In this definition, both and are values for the Earth-Sun distance at the time of measurement. However, this is numerically the same as what would be obtained if both and were corrected to the mean Earth-Sun distance by factors applied to each, because the correction factors on and cancel out. That is to say, the irradiance at the sea surface for Earth-Sun distance is
| (5) |
It thus follows that
| (6) |
Another way to view is to think of it as the bidirectional reflectance distribution function (BRDF) of the ocean normalized by the BRDF of a perfectly reflecting Lambertian surface. The BRDF of a surface as measured in the laboratory is the radiance reflected by the surface divided by the incident plane irradiance onto the surface. The BRDF of a Lambertian surface whose irradiance reflectance is is , with units of inverse steradian. For a perfect Lambertian reflector, , and
This makes it clear that the carries units of solid angle, so that is nondimensional.
The BRDF Effect
As noted above, the normalizations contained in or remove the effects of solar zenith angle, atmospheric attenuation, and Earth-Sun distance on a measured radiance . However, still refers to a particular viewing direction . This dependence ties to the angular distribution of the upwelling underwater radiance and to the transmittance through the sea surface from water to air (which depends on the wave state, i.e., on the wind speed). The upwelling underwater radiance in turn depends on the angular distribution of the incident sky radiance, surface transmittance from air to water, and to the absorbing and scattering properties of the water body (the scattering phase function in particular). The dependence of the upwelling radiance distribution on the sky radiance distribution, viewing geometry, and water optical properties is commonly called the BRDF effect. The final step is to remove the BRDF effect to the greatest extent possible.
The BRDF effect was studied by Morel and colleagues in a series of papers, Morel and Gentili (1991), Morel and Gentili (1993), and Morel and Gentili (1996), culminating in Morel et al. (2002). They used numerical radiative transfer models to compute correction factors that would transform a measurement made for a particular Sun zenith angle, viewing direction, wind speed, atmospheric conditions, and water IOPs into a measurement that corresponds to a zenith Sun and nadir viewing direction for a typical marine atmosphere and for Case 1 water with a given chlorophyll value. The correction involves three separate factors, , , and , as follows.
Let be a nondimensional factor that accounts for all transmission and reflection effects by the wind-blown sea surface when is transmitted downward through the surface to give , and is transmitted upward through the surface to give . Polar angle (measured from the nadir) is the underwater angle that is refracted by the surface into the above-surface viewing direction of the water-leaving radiance . is the wind speed. depends on the wind speed (i.e., the surface wave state) and the water index of refraction via the Snel’s law mapping of to . However, Gordon (2005) showed that the dependence of on wind speed is very weak, and usually can be computed with adequate accuracy over a wide range of viewing angles using . The detailed derivation of in Morel and Gentili (1996) (Eq. 5 and Appendix D) shows that, strictly speaking, also depends on the solar zenith angle and the angular distribution of the incident atmospheric radiance, which affect how much incident irradiance is transmitted through the sea surface. Likewise, depends on the water IOPs via the in-water irradiance reflectance . However, these dependencies are weak compared to the directional () dependency and so, for compactness and consistency with Morel’s notation, are not shown as arguments.
Let be the reference value of corresponding to transmission normal to the mean sea surface (). Multiplying the of Eq. (2) by corrects for surface-transmission effects for the actual viewing direction and wind speed . For , ; is greater than 0.52 out to angles of 50 deg. Note that Figure 4 of Morel et al. (2002), which shows ratios of , was incorrectly computed; see the discussion and revised figures in Gordon (2005).
The dimensionless factor is defined by , where and are the water absorption and backscatter coefficients, respectively, which are assumed homogeneous for the present discussion. This factor parameterizes how downwelling irradiance in the water is converted to upwelling irradiance by backscatter and reduced by absorption. That is to say, relates the irradiance reflectance within the water to the most relevant IOPs. values are in the range of 0.3 to 0.5 (Morel and Gentili (1996), Fig. 2).
The factor (units of steradian) describes the angular distribution of the upwelling radiance. for an isotropic upwelling radiance distribution; actual in-water radiance distributions typically have values in the range of 3 to 6 sr (Morel and Gentili (1996), Fig. 3).
In practice, and are combined to give a term that has less variability than the individual factors. The combined factor describes how the downwelling irradiance just beneath the sea surface is reflected back upward as upwelling radiance in the direction (). The term thus describes both the efficiency of conversion of downwelling irradiance into upwelling radiance, and the angular (non-isotropic) distribution of the upwelling underwater radiance that generates the water-leaving radiance. values are typically in the range to 0.07 to 0.15 (Morel and Gentili (1996), Fig. 6). Let refer to the ratio for the nadir viewing direction and Sun at the zenith.
Multiplying by corrects for the difference of the actual angular distribution of the upwelling radiance and what that distribution would be for the Sun at the zenith, nadir viewing, for the particular atmospheric and oceanic conditions used to compute and .
Applying these BRDF corrections to the of Eq. (2) gives (Morel et al. (2002), Eq. 13):
| (7) |
Morel et al. call the ”exact normalized water-leaving radiance.” The arguments “ATM” and “IOP” refer to the specific set of atmospheric conditions and water inherent optical properties used to compute and . (As previously noted, these arguments are omitted from the terms because the ATM and IOP dependencies are small for .) This is equivalent to the normalization seen in Eq. (2) of Franz et al. (2007), except for a sensor-specific correction factor for out-of-band wavelength response. It should be noted that the factor has arguments of () because those values correspond to the same atmospheric and oceanic conditions as the factor; the difference is that corresponds to and . Values of the product are typically in the 0.6 to 1.2 range, depending on the IOPs, solar zenith angle, atmospheric conditions, wind speed, and wavelength.
It is noted that the wind speed at the time of observation, , is shown in both the and terms in Eq. (7). It can be argued that these terms should use a reference value of , so that all quantities are referred to a level sea surface. However, as presently implemented by the OBPG, the same wind speed is used in the reference terms.
The atmospheric conditions used to compute the factors were typical of marine atmospheres and are summarized as follows (Morel and Gentili (1996); Morel et al. (2002)):
- The atmosphere was modeled as 50 layers, each 1 km thick
- The aerosol optical thickness was at 550 nm.
- The tropospheric aerosols had a relative humidity of 70% and were distributed in the upper 45 atmospheric layers
- The marine aerosols had a relative humidity of 90% and were distributed in the lower 5 atmospheric layers
- The aerosol phase functions were modeled using Mie theory and the data of Shettle and Fenn (1979).
- The sea surface was modeled using a Gaussian distribution of wave slopes based on the empirical wind-speed, wave-slope data of Cox and Munk (1954b) (page 847) for the given wind speed . was taken to be 0 for the calculations, although there are still some residual capillary waves according to the empirical slope data of Cox and Munk.
The water optical properties were obtained from bio-optical models for Case 1 water, for which the IOPs can all be parameterized by the chlorophyll concentration . In particular, the scattering phase function was computed as a chlorophyll-weighted sum of phase functions for “small” and “large” particles, which themselves were computed using T-matrix theory for non-spherical particles with different size distributions. The details of the IOP bio-optical models are given in Morel et al. (2002).
The radiative transfer calculations were carried out using a Monte Carlo code for calculation of the factors, and using HydroLight for the calculations. The are tabulated for an exactly level sea surface and for wind speeds of and ; the values include a small amount of residual capillary waves because the Cox-Munk mean square sea surface slopes are not extactly zero for a zero wind speed. The calculations were done both with and without Raman scattering by water. None of the calculations included polarization. These codes were run for
- 7 wavelengths (412.5, 442.5, 490, 510, 560, 620, and 660 nm)
- 6 chlorophyll values ( = 0.03, 0.1, 0.3, 1.0, 3.0 and ). The water was homogeneous.
- 6 solar zenith angles ( = 0, 15, 30, 45, 60 and 75 deg)
- 13 azimuthal angles ( = 0 to 180 deg by steps of 15 deg)
- 17 nadir angles ( = 1.078, 3.411, 6.289, 9.278, 12.300, 15.330, 18.370, 21.410, 24.450, 27.500, 30.540, 33.590, 36.640, 39.690, 42.730, 45.780, and 48.830 deg)
These runs give a total of values, which are organized into tables, each with 13 columns and 17 rows. A separate table gives values of at increments of 1 deg and for wind speeds of and . The tables including Raman effects are available at BRDF tables.
Use of these tables requires the chlorophyll concentration, which is not a priori known. In the initial study of Morel and Gentili (1996), a band-ratio algorithm was used to obtain an initial guess for . That value was then used in the tables to obtain the BRDF correction factors. Those factors give a new estimate of , which can be used to obtain an new value of , and so on. However, the tables are not tied to how the value is obtained, so in practice any algorithm can be used to obtain values from the reflectances in an iterative process.
Finally, the exact normalized water-leaving radiance of Eq. (7) is used in Eq. (3) to obtain the exact normalized water-leaving reflectance:
The quantities in brackets can all be obtained from pre-computed look-up-tables given the Sun and viewing geometry, wavelength, atmospheric conditions used to obtain from (used to determine ), and the chlorophyll concentration. The chlorophyll concentration determines the IOPs according to the bio-optical models for Case 1 water used in the Morel et al. calculations.
Although Morel and others call the “exact” normalized water-leaving radiance, and the “exact” normalized water-leaving reflectance, it must be remembered that these quantities are exact only if the atmosphere and ocean have exactly the same absorbing and scattering properties as used in the model simulations upon which the BRDF correction factors are based. That will of course not in general be the case. In Case 1 waters, the differences between the Morel et al. Case 1 IOP model and the actual ocean IOPs are often small enough that the BRDF-corrected quantities are sufficiently accurate for remote sensing. However, the differences can become large in Case 2 waters. Research therefore continues on ways to improve the BRDF correction, both to extend its validity to Case 2 water and to remove the need to estimate the chlorophyll concentration in order to use the look-up tables (Lee et al. (2011), Fan et al. (2016)). Although further improvements can be anticipated, the BRDF correction as described above remains the OPBG operational algorithm at the time of this writing.
The OBPG works with radiance to get to . However, when doing atmospheric correction on TOA radiances, the various look-up-tables used for Rayleigh correction, etc. are in terms of reflectances . Equation (8) allows easy conversion from one to the other, depending on which quantity is most convenient for a given step of the atmospheric correction process.
It is to be noted that the “remote-sensing reflectance” reported by the NASA OBPG as a standard Level 2 product of the NASA ocean color satellites such as MODIS and VIIRS is the exact normalized water-leaving reflectance of Eq. (9), divided by :
| (10) |
However, the “remote-sensing reflectance” computed by HydroLight is as defined by Eq. (4). A given HydroLight run computes for all viewing directions for the given and other conditions of wind speed, IOPs, and atmospheric radiance distribution. Thus the HydroLight outputs for various viewing directions incorporate the BRDF effects. (Indeed, comparison of HydroLight-computed values with HydroLight values for a zenith Sun and nadir viewing direction is how the BRDF factors were determined in the Morel et al. studies.) Thus there is no need for an explicit BRDF correction to the HydroLight-computed . If a HydroLight run has the Sun at the zenith, then the nadir-viewing HydroLight times corresponds to :
| (11) |
Recalling Eq. (10), this gives
| (12) |
There should be only a very small difference in HydroLight’s and , attributable to any differences in the angular distributions of the sky radiances used to compute the Morel BRDF factors and as used in HydroLight. Morel et al. (2002) (page 6295) notes that these differences are negligible.
It should be noted that HydroLight values are valid for whatever IOPs were used in the run; there is no restriction to homogeneous Case 1 water and no need to estimate a chlorophyll concentration as must be done when applying the Morel BRDF factors. Thus HydroLight can give a very general via Eq. (11), without the assumptions made by Morel et al. when developing the BRDF correction factors seen in Eq. (9).
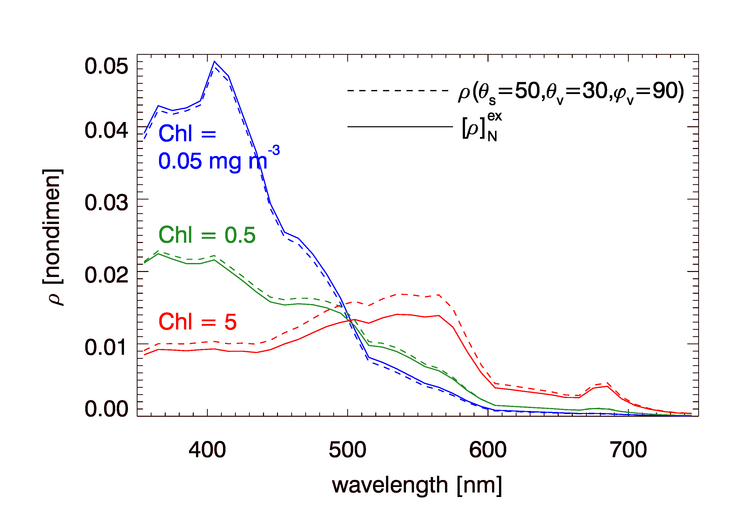
Figure 2 illustrates the magnitudes of the corrections to values. HydroLight was first run to generate remote-sensing reflectances for a Sun zenith angle of deg, with the Sun in a clear sky. The water IOPs and chlorophyll values were the same as those used for Fig. 1. The runs included Raman scatter by water and fluorescence by chlorophyll and CDOM. The dashed lines in Fig. 2 show the values of . These viewing angles correspond to a sensor viewing the ocean at an off-nadir angle of 30 deg at right angles to the solar plane. The HydroLight runs were then repeated with the Sun at the zenith. The solid lines in the figures show the resulting values of as determined by Eq. (11). Depending on the water IOPs, Sun zenith angle, viewing direction, and wavelength, the normalization can change a spectrum by tens of percent, or almost not at all. The changes tend to be greatest in high-chlorophyll waters, at large solar zenith angles, and at large off-nadir viewing angles.
When formulated in terms of reflectances, the partitioning of Eq. (3) of the Problem Formulation page becomes (e.g., Gordon and Wang (1994a))
| (13) |
where the terms correspond to those of Eq. (3) of that page. A similar equation applies to the reflectance form of Eq. (4) of the Problem Formulation page.
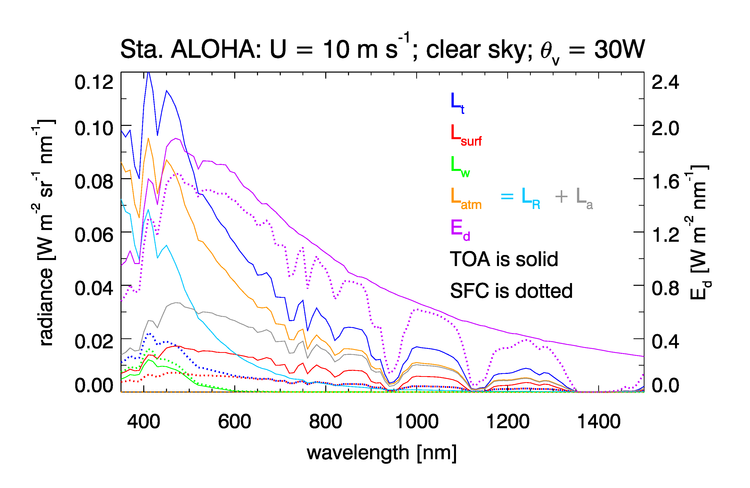
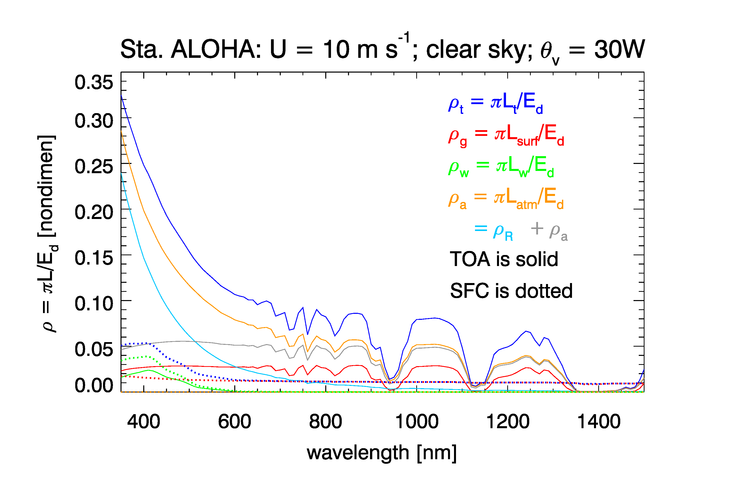
Figure 4 shows the radiances shows the radiances of Fig. 2 of the previous page. Figure 4 shows these radiancesrecast as normalized reflectances. It should be noted in Fig. 4 that the solar-spectrum features (most noticeable below 600 nm) seen in the TOA spectrum of Fig. 3 are removed by the normalization process. However, the atmospheric absorption features (most noticeable beyond 600 nm) remain in the TOA reflectances, but are not present in the surface reflectances. Thus the dotted curves for , , and , are very smooth functions of wavelength. The surface glint reflectance spectrum is almost independent of wavelength, whereas the surface glint radiance seen in Fig. 3 depends of wavelength in the same manner as the surface irradiance spectrum. (Note that the glint reflectance considered here is not the same as the surface radiance reflectance factor of Mobley (1999) Eq. 4, and Mobley (2015), which is a ratio of reflected to incident sky radiances for the given wind speed, and Sun and viewing directions.)
Summary
The interpretation of as developed above can be summarized as follows:
- Start with a measured . Then
- The division by in Eq. (2) moves the Sun to the zenith.
- The division by in Eq. (2) rescales the radiance magnitude to account for atmospheric attenuation, but the angular distribution of the radiance is unchanged. This diffuse transmission is for the actual atmosphere at the time of observation.
- The factor in Eq. (2) corrects for the Earth-Sun distance.
- The BRDF factors in Eq. (7) normalize as measured for the actual atmospheric and in-water radiance distributions to what would be for a reference atmospheric radiance distribution and for Case 1 water with the given chlorophyll value.
The proposed atmospheric retrieval accuracy requirements for the PACE (Pre-Aerosol, Clouds, and ocean Ecosystem) mission are (Franz (2015))
- for in the 350-400 nm range, a maximum error of 0.002 or 10%
- for in the 400-710 nm range, a maximum error of 0.001 or 5%
In terms of , this gives
- for in the 350-400 nm range, a maximum error of
- for in the 400-710 nm range, a maximum error of
Given that the water-leaving radiance is at most 10% of the TOA radiance (e.g., Fig. 3 of the previous page), a requirement for a 5% maximum error in (expressed as the same percentage error in or ) implies a maximum error of roughly 0.5% in the measured TOA radiance . Such a small error in the TOA radiance cannot be achieved by pre-launch sensor radiometric calibration alone. Thus ocean color sensors require post-launch “vicarious calibration.” This term refers to the process of (1) performing atmospheric correction to recover sea-level spectra from the measured ; (2) propagating the corresponding sea-level back to the TOA (including the atmospheric path radiance contributions) to obtain a TOA radiance for comparison with the sensor-measured TOA radiance . The difference between the retrieved and the measured then (3) gives a final set of sensor calibration correction factors to be applied to the measured TOA radiances so that they lead, after atmospheric correction, to the proper sea-level water-leaving radiances and associated reflectances.
The part of the Morel et al. correction has been validated against empirical data for Case 1 waters by Voss et al. (2007) and found to give good agreement with measured radiance distributions. As concluded there, “...the bidirectional corrections based on the lookup tables generated from the model, and presently applied to ocean color imagery, are sound and amply validated for Case 1 waters...” However, it should be remembered that the above BRDF correction is based on a particular atmospheric model and on particular bio-optical models for Case 1 water. For different atmospheric conditions, the correction would be different, although the difference would probably be small. However, for different water IOPs, in particular for Case 2 waters with high mineral particle loads or high concentrations of CDOM, the differences in the water-column scattering and absorption properties could have a significant effect on the correction. That variability has not yet been studied, and the above correction remains the current state of the science and is implemented by the OBPG for operational ocean color image processing.

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.