Page updated:
July 7, 2022
Author: Curtis Mobley
View PDF
The Nature of Light
Writing this page is a no-win effort. No matter what I say about the “nature of light” or the question “What is a photon?”, there will be those who tell me (quite correctly!) that I am wrong. However, the question “What is light?” is perfectly legitimate and deserves discussion, even if, as will be seen, there is no answer in everyday, human, classical physics terms.
This page is structured as a chronological “history of light” organized around the debate about whether light is a particle or a wave. Some of the milestones in our understanding of light warrant just a sentence or two; others will be discussed in some detail.
- ancient Egypt
- Light is “ocular fire” from the eye of the sun god Ra.
- ancient Greece
- Democritus (c. 500 BCE) speculated that everything, light and the soul included, is made of particles, which he called atoms. Other Greeks thought that light was rays that emanate from the eyes and return with information. I haven’t seen any explanation of how they explained why everyone’s eyes quit emanating rays when the sun went down, or when a person entered a dark cave. Somewhat later, Aristotle thought that “light is the activity of what is transparent.” In his view, light is a “form,” not a “substance.” I don’t know if he thought that things became nontransparent when it got dark at night.
- c. 1000 CE
- Ibn al-Haytham (965-1039; Latinized as Alhazen): Light is rays that travel in straight lines. Little known today in the West, Ibn al-Haytham was something of an Arab Isaac Newton. He wrote a seven-volume Book of Optics (as well as many other works on astronomy, mathematics, medicine, philosophy, and theology). He clearly understood the “scientific method” and he based his conclusions on observation and clever experiments, rather than on abstract reasoning. He disproved the Greek idea that light emanates from eyes, and he showed that light travels in straight lines.
- late 1600s
- Newton: Light is particles. Isaac Newton conducted a series of experiments in the late 1600’s which, among other things, showed that white light is a mixture of all colors. This directly contradicted Aristotle, who claimed that “pure” light (like the light from the Sun) is fundamentally colorless. Because he was able to separate while light into colors with a prism, and because light did not seem to travel around corners (as do sound waves), Newton concluded that light must be made of particles, which he called “corpuscles.” He published his results in his treatise Opticks in 1704. Newton’s particle explanation of refraction required light to travel faster in water than in air, and his explanation of “Newton’s rings” (easily explained by wave interference) was rather incoherent (pun intended). In spite of a few errors like these, Newton was a pretty good scientist and Opticks is one of the seminal books of science.
- 1676
- Ole Rømer measured speed of light by timing eclipses of Jupiter’s moon Io.
- 1678
- Christiaan Huygens published the first credible wave theory of light. Part of his theory says that at each moment each point of an advancing wave front serves as a point source of secondary spherical waves emanating from that point. The position of the wave front at a later time is then the tangent surface of the secondary waves from each of the point sources. This known as Huygen’s principle.
- 1803
- Young: Light is waves. In 1803 Thomas Young conducted a classic
experiment (published in 1807) in which coherent light was incident
onto two narrow parallel slits in an opaque screen as illustrated in Fig.
1. According to Huygen’s principle, each slit is the source of secondary
waves, which then interfere with each other as they propagate further.
The light that passed through the slits formed an interference pattern
on a viewing screen, just as do water waves passing through holes in
a board. This is easily explained by assuming that light is a wave
phenomenon. Young’s double-slit experiment was taken as conclusive
proof that light is a wave and that Newton was wrong. As will be seen
below, this conceptually simple double-slit experiment will reveal one
of the most profound mysteries of light.
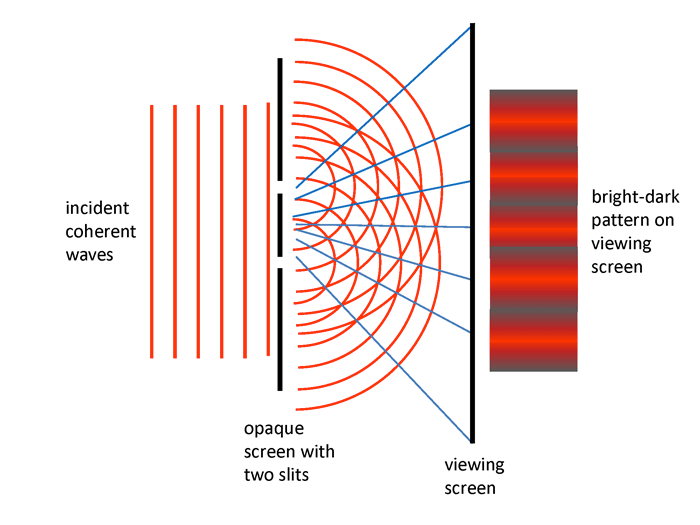
Figure 1: The essence of Young’s double-slit experiment. Coherent means that the monochromatic incident light has the wave crests “in step.” The blue lines show the points along which the crests of the red light waves add together to create bright bands on the viewing screen.
- 1819
- Poisson, Fresnel, and Arago: Light is waves. In 1818, Augustin-Jean
Fresnel presented a new theory of diffraction. Siméon Poisson, who favored
Newton’s corpuscular theory of light, analyzed Fresnel’s equations and
concluded that if they were correct, then the shadow of a sphere illuminated
by a point light source would show a spot of light at the center of the
shadow. Poisson considered this an absurd result, thereby disproving
Fresnel’s assumption of the wave nature of light. However, when Dominique
Arago did the experiment, the spot was there just as predicted, as seen in
Fig. 2. Poisson conceded. This point of light is now known as Fresnel’s
spot, Arago’s spot, or—no doubt to his chagrin—Poisson’s spot.
Again, as in Young’s experiment, light must be understood as a
wave.

Figure 2: Fresnel’s Spot at the center of the shadow of a 2 mm diameter sphere at a distance of 1 m from the sphere. The sphere was illuminated by a 633 nm laser. Image from Wikipedia
- 1865
- Maxwell: Light is electric and magnetic fields propagating as a wave. In 1864 James Clerk Maxwell published A Dynamical Theory of the Electromagnetic Field in which he tied together electric and magnetic fields via his famous equations. He then showed that each component of the electric and magnetic fields obeys a wave equation with a speed of propagation numerically equal to that of light. He concluded “This velocity is so nearly that of light that it seems we have strong reason to conclude that light itself (including radiant heat and other radiations) is an electromagnetic disturbance in the form of waves propagated through the electromagnetic field according to electromagnetic laws.” (This has to be one of the greatest sentences ever written.) Maxwell’s equations are discussed beginning at Maxwell’s Equations in Vacuo.
- late 1880s
- Hertz: Discovery of radio waves. Between 1886 and 1889
Heinrich Hertz conducted a series of experiments designed to test Maxwell’s
predictions of propagating electromagnetic waves. In these experiments
Hertz discovered what are now called radio waves, and he also discovered
the photoelectric effect.
Young’s double-slit experiment, Arago’s confirmation of the Fresnel diffraction predictions, and Hertz’s confirmation of Maxwell’s predictions of propagating electromagnetic waves were sufficient to convince everyone that light is a wave. Newton was clearly wrong, and the matter seemed settled once and for all.
- late 1800s
- Blackbody radiation. One of the final problems of late nineteenth century physics was to explain the spectral distribution of energy emitted by a “blackbody.” Attempts to do this using Maxwell’s concept of electromagnetic radiation led to the prediction that a blackbody would emit an infinite amount of energy as the frequency increased. This unphysical result was called “the ultraviolet catastrophe.”
- 1901
- Planck: The idea that light is quantized. Max Planck was able to derive
the formula for the blackbody radiation spectrum, but only if he assumed that
light comes in discrete packages, or “quanta.” He had to assume that the energy
of each light quantum is proportional to its frequency
or
wavelength
according to
The proportionality constant , which occurs both in this equation and in Planck’s formula for the energy distribution of blackbody radiation, was a free parameter that was adjusted so that Planck’s blackbody spectrum would fit the measurements. The parameter is now called Planck’s constant and is one of the fundamental physical constants. Planck himself could not say why the radiation in the blackbody cavity should come in discrete pieces and, at the time, he thought that this assumption was perhaps just “a mathematical artifice.” Planck received the 1918 Nobel Prize in Physics for this work; the Nobel citation credits him with the “discovery of energy quanta.” His discovery was the beginning of modern physics.
- 1905
- Einstein: showed that light really is quantized and is absorbed in
discrete amounts. The photolectric effect discovered by Hertz can not be
explained if light comes in continuous waves as proposed by Maxwell. Albert
Einstein was able to explain the photoelectric effect by assuming
that light does indeed come in discrete packages as hypothesized by
Planck and that these quanta are absorbed (or emitted) “all at
once,” rather than being “soaked up” bit by bit as a continuous
light wave arrives at the surface of the photoelectric material. In
other words, Einstein claimed that energy quanta were real physical
quantities, and not just a mathematical trick. As he worded it in his
1905 paper, “Energy, during the propagation of a ray of light, is not
continuously distributed over steadily increasing spaces, but it consists of a
finite number of energy quanta localized at points in space, moving
without dividing and capable of being absorbed or generated only as
entities.”
Einstein’s claim that light comes in discrete packets was not well received at the time because the wave theory of light was so well established and had been so successful in most applications—blackbody radiation and the photoelectric effect being the exceptions. In the same year, Einstein also published his famous paper presenting the special theory of relativity; an explanation of Brownian motion, which helped established the reality of atoms at a time when many scientists still did not accept their existence; and a paper presenting the equivalence of mass and energy via his most famous equation, . His claims of light as particles, the mixing of time and space, matter as particles, and the equivalence of matter and energy would have relegated Einstein to the realm of crackpots had his radical ideas not been so successful in explaining so many physical phenomena. When he received the Nobel Prize in 1921 special relativity was still so controversial that the award was given to him for “his discovery of the law of the photoelectric effect.”
- 1923
- Compton scattering: light is a particle. In 1923 Arthur Compton did
an experiment in which he bombarded electrons with x-rays. Figure 3 shows
the basic idea. Compton found that the incident x-ray wavelength
and the
wavelength
of the scattered x-ray were related to the mass of the electron
and the
angle
of the scattered x-ray from the initial direction by the formula seen in
the figure. This formula is derived by assuming that the x-ray is a
particle of zero rest mass and energy given by Planck’s formula
,
and then applying the equations for relativistic conservation of energy and
momentum.
Compton scattering cannot be explained by a wave theory of light. This result therefore was taken to be direct experimental evidence that light is a particle. Compton received the 1929 Nobel Prize in Physics for this work.
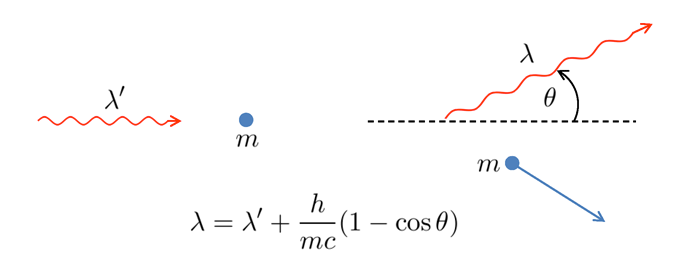
Figure 3: Compton Scattering. The left panel shows an x-ray quantum approaching a stationary electron. The right panel shows the scattered x-ray and electron.
- 1926
- The name “photon” was coined by the chemist G. N. Lewis to describe a hypothetical particle that transmitted energy from one atom to another. The word caught on as a name for Einstein’s quantum of energy, although that is not what Lewis intended.
- The 1910s to 1930s
- The development of quantum mechanics.
These decades were a time of great excitement (and confusion!) in
physics. On the one hand, there were convincing experiments showing
that light is a wave: Young’s double-slit experiment, Fresnel’s spot,
and Hertz’ discovery of electromagnetic waves just as predicted by
Maxwell’s wave theory of light. On the other hand, there were equally
convincing experiments showing that light must be a particle of
some kind: the photoelectric effect, Compton scattering, and the
need to assume light quantization in order to explain blackbody
radiation.
The physics vocabulary now began to include phrases such as “the wave-particle duality of light” (and, indeed, of all matter). The idea is that light has both wave and particle properties and that you detect one or the other depending on the type of measurement being made. That is, if you set up an experiment that is designed to detect wave properties (e.g., a double-slit apparatus), then you will detect light as a wave. But if you set up an experiment that absorbs or emits light (e.g., the photoelectric effect), then you will detect it as discrete quanta or particles. You will also see statements such as
- Light behaves as a wave at macroscopic scales (e.g., in a laboratory interference experiment), but it behaves as a particle at atomic scales (e.g., in Compton scattering).
- Light behaves as a wave at low energies (no radio engineer ever talks about radio photons, just radio waves), but it behaves as a particle at high energies (those working with gamma rays always talk about gamma-ray photons, never gamma-ray waves).
- Light propagates as a wave (according to Maxwell’s equations), but it interacts with matter as a particle (e.g, in the photoelectric effect or in Compton scattering).
There is an element of truth to all of these statements, but they also all oversimplify the true nature of light by forcing it to fit into classical categories of wave or particle.
During these decades the great physicists Bohr, Schrödinger, Heisenberg, Pauli, Dirac and many others developed an entirely new kind of physics—quantum mechanics—to describe the internal workings of atoms. This quantum mechanics is a theory of how matter behaves at the atomic scale. Energy levels in atoms and molecules are quantized, and atoms and molecules therefore absorb and emit energy only at specific frequencies determined by differences in the quantized energy levels of each kind of atom or molecule. Electromagnetic radiation was thus absorbed or emitted only at the discrete frequencies determined by the quantized energy levels of matter, but the radiation itself did not need to be treated as inherently quantized. A good layman’s history of this era is Thirty Years that Shook Physics by George Gamow.
- 1946
- An unexpected result in the Hydrogen spectrum. Willis Lamb and Robert Retherford measured an extremely small difference in the energies of the and states of the Hydrogen atom (see the page on the Physics of Absorption for a discussion of energy levels and this notation). This energy difference corresponds to a wavelength of about 30 cm, which is in the microwave region of the electromagnetic spectrum. Now known as “the Lamb shift”, this difference in energy levels could not be explained either by the non-relatavistic quantum mechanics of Schrödinger and Heisenberg, or by the relativistic quantum mechanics developed by Dirac. This experiment was one of the driving forces behind the development of quantum electrodynamics. Lamb received the Nobel Prize in 1955 “for his discoveries concerning the fine structure of the hydrogen spectrum.”
- late 1940s
- The development of Quantum Electrodynamics (QED). In
QED, light is particles, but very strange particles they are. In part to
explain the Lamb shift, Richard Feynman, Julian Schwinger, Shinichiro
Tomonaga, and several others developed what is now known as Quantum
Electrodynamics or QED. Feynman, Schwinger, and Tomonaga shared the
1965 Nobel Prize in Physics for their development of QED. In this theory,
the electromagnetic field itself is quantized. Moreover, in QED the electric
field of an electron, for example, is caused by the electron emitting and
reabsorbing enormous numbers of energy quanta, which are called virtual
photons. These photons are called virtual photons because they are
associated with undetectable energy states of the electron-photon
system.
The Heisenberg uncertainty principle can be written as . To detect an energy change of size , you must observe the system for a time that is greater than . The emission of a virtual photon of energy by an electron violates conservation of energy, but this is allowed by the Heisenberg uncertainty principle so long as the virtual photon is reabsorbed within a time of . That is, you can violate conservation of energy so long as you don’t do it long enough to get caught. Or in another view, you are not really violating conservation of energy if the violation isn’t observable. A photon can travel a distance before it is reabsorbed by the electron. Thus low energy virtual photons with a small can live longer and “reach out” farther from the electron before reabsorption than higher energy virtual photons, which exist for a shorter time. This gives rise to the strength of the classical electrical field as seen in Coulomb’s law. Similarly, a photon can turn into an electron-positron pair so long as the electron and positron reunite before the time limit imposed by Heisenberg’s relation. Note that the emission of virtual photons is a different process than the emission of photons when an atom changes energy levels and emits a photon with energy equal to the difference of the atomic energy levels. In that case, there is no energy violation, Heisenberg’s relation does not come into play, and the emitted photon can live forever (or until it is absorbed by a different atom somewhere else).
In QED, a charged particle is surrounded by a cloud of virtual photons, which are constantly flickering in to and out of existence. When two charged particles approach each other, some of these virtual photons are exchanged between the particles, which is what gives the repulsive or attractive force of between the particles. The electric force is said to be “mediated” (i.e., transmitted) by the exchange of virtual photons. (In modern physics, all “action at a distance” forces (except perhaps gravity) are mediated by some type of particle. For electric forces the particles are photons.) Indeed, even “empty space” is seething with virtual particles that come into existence and then promptly disappear.
QED is able to explain the Lamb shift because the and states interact slightly differently with the cloud of virtual photons surrounding the Hydrogen nucleus and electron. This quantitative explanation of the Lamb shift was one of the first tests of QED. There have been many more since, and some of QED’s predictions agree with experiment to within about one part in . QED is therefore considered the most successful and well tested theory in physics, and it is the starting point for all of elementary particle physics.
- late 20th century
- The Fundamental Mystery: single-photon interference
in a double-slit experiment. The interference patterns seen in Young’s
double-slit experiment can be understood in terms of classical wave theory
when the incident light is a coherent wave. But what happens if only one
photon at a time is incident onto the double-slit screen? Amazingly, you still
get the same interference pattern! It takes longer to build up the
pattern one photon at a time, but after many photons have been
detected (e.g., on a CCD array), the pattern becomes obvious. There
is an excellent video of an 1981 verification of this performed at
Hamamatsu Photonics K.K., a company that makes optical sensors and
instruments. This video is on the Hamamatsu web site and also on
Youtube at https://www.youtube.com/watch?v=I9Ab8BLW3kA.
This video is well worth ten minutes of your time. It also shows
how the experiment was actually conducted. (I don’t know who
first did an experiment like the one on the Hamamatsu web site.
However, in 1909 G. I. Taylor conducted an experiment in which
he showed that a very faint light source, equivalent to “a candle
burning at a distance slightly exceeding a mile,” gave interference
fringes.)
Figure 4 shows four frames from the Hamamatsu video. In Fig. 4(a), photons have been collected one at a time for 3 minutes. Only about two dozen photons have been detected, and the pattern of dots, showing where each photon was detected on the detector screen (as illustrated in Fig. 1) appears to be random. A few minutes later (panel b) more photons have been detected, but no pattern is yet obvious. However, after 25 minutes (panel c) enough photons have been detected that an interference pattern is taking shape. After 6 hours, the pattern of individual photon detection locations clearly shows exactly the same interference pattern as is obtained for a bright source of coherent monochromatic light.
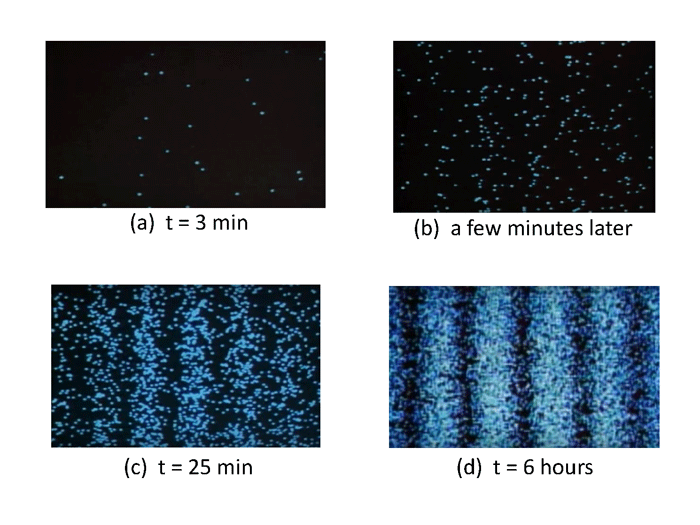
Figure 4: Locations of photon detections on the observing screen of a double-slit apparatus showing the build-up of an interference pattern by single photons. Frames captured from the Hamamatsu video.
In classical wave theory (such as in Young’s original experiment), part of the incident wave passes through each slit, and each slit then becomes a point source for waves that propagate further (Huygen’s principle) and interfere with each other as illustrated in Fig. 1. The fact that single photons also show interference patterns after enough are collected implies that the individual photons must also simultaneously pass through both slits and then interfere with themselves! Indeed, if you modify the experiment so that the photon can pass through just one slit, or that you can in some way even know which slit it went through, then the interference pattern disappears. The fact that single photons show an interference pattern is so surprising and incomprehensible from the viewpoint of classical physics, that the great physicist and teacher Richard Feynman calls this “The Fundamental Mystery” (of quantum mechanics). There is no explanation for this other than to say “this is just how photons behave.”
There are two utterly profound consequences of single-photon interference:
- We are forced to abandon the idea that photons are localized particles in the classical sense of having a well-defined (even small) size. A localized particle could not pass through both slits at the same time and then interfere with itself.
- We are forced to abandon the idea that photons take a particular path from one point to another. In QED calculations (using so-called Feynman path integrals), a photon simultaneously takes all possible paths from one point to another. Only after all of the calculations are done for all possible paths and the results for the different paths are combined does the final result look like the classical idea of a light ray traveling from one point to the next by a single path.
For a photon, concepts like size, position, and path are undefined and meaningless. All you can say is that a photon was created at point A (e.g., at a spot on the surface of a tungsten filament in a light bulb) and it was detected at point B (e.g., at a particular pixel of a CCD array). You can say nothing about the path it took from A to B. (In quantum mechanics, there is no position operator for photons, as there is for material particles like electrons. Instead, photons have creation and annihilation operators which create and destroy them.)
To make matters even more mysterious, material particles such as electrons and atoms also display the same interference behavior as light in a double slit apparatus. Single electron interference was first demonstrated in 1989 (Tonomura et al. (1989)). The interference patterns in their experiment look exactly like the ones in Fig. 4, except that the points show where the individual electrons were detected rather than where individual photons were detected. This experiment has since been repeated with molecules of more than 800 atoms and molecular weights greater than amu (Eibenberger et al. (2013)). These experiments are strong verifications of the correctness of quantum mechanics as currently formulated.
Feynman wrote a delightful and highly recommended book, QED: The Strange Story of Light and Matter (Feynman (1985)). This book explains, as only Feynman can, the fundamental ideas of QED without the math. He clearly considers light to be particles. For example, (on page 15 of my edition) he states “It is very important to know that light behaves like particles, especially for those of you who have gone to school, where you were probably told something about light behaving like waves. I’m telling you the way it does behave—like particles.” However, he also shows that these mysterious particles actually do take all possible paths from one point to another. Thus a photon goes through both slits because each slit is a possible path from the point of the photon’s creation to the point where it is detected. (If you want to see the mathematical horrors of how QED calculations are performed, the best book I’ve found is Introduction to Elementary Particles by David Griffiths (Griffiths (2008)). However, that book presumes you have spent some serious years in physics and math classes.) In 1979 Feynman also delivered a series of non-technical lectures on QED at the University of Auckland, which were the origin of his QED book. These are well worth viewing and are on-line in various places, e.g., at http://www.vega.org.uk/video/programme/45.
Most physicists today seem quite happy talking about photons as one member of the pantheon of “elementary particles.” In their language, photons are zero-rest-mass, stable, spin one bosons, which always travel at the speed of light and have energy , momentum of magnitude , and angular momentum of magnitude .
However, some people view things differently. Willis Lamb, of Lamb shift fame, wrote a paper “Anti-photon” (Lamb (1995)) in which he states “In his [the author Lamb’s] view, there is no such thing as a photon. Only a comedy of errors and historical accidents led to its popularity among physicists and optical scientists. There are good substitute words for ’photon’, (e.g., ’radiation’ or ’light’)....” In closing he says, “It is high time to give up the use of the word ’photon’, and of a bad concept which will shortly be a century old. Radiation does not consist of particles, and the classical, i.e., non-quantum, limit of QTR [the quantum theory of radiation, or QED] is described by Maxwell’s equations for the electromagnetic fields, which do not involve particles.”
Lamb’s paper is worth reading, and he makes some valid points. However, I’m afraid his battle to banish the word “photon” is lost. It is just too convenient. Biologists are going to continue to measure the light available for photosynthesis in units of photons per square meter per second. One einstein is going to retain its definition as “one mole of photons.” Optica (previously The Optical Society of America) is going to continue to publish Optics & Photonics. (Indeed, that magazine devoted the entire issue of October 2003 to six articles on the topic of “What is a Photon?”) It certainly would have been fun to get Lamb and Feynman together in a room and watch them argue about the reality or non-reality of photons. Perhaps the greatest danger inherent in the use of the word “photon” is that it makes it easy to think of light as little balls of energy behaving like particles in the every-day sense, which simply is not correct, as we have seen above.
My own concession to Lamb and to the inability to say that a photon takes a particular path from point A to point B is that my Monte Carlo codes no longer “trace photons;” they now “trace rays.” The concept of a light ray is well accepted in the limit of geometrical optics, and all camera lenses are designed with sophisticated ray tracing codes that give perfectly good predictions of what light does, as do my Monte Carlo codes. My Monte Carlo calculations remain unchanged, I’m just more careful in describing what they do.
- The present day
- Enough has been said. The above discussion has reviewed the
long and confused history of ideas about the nature of light. Our
understanding of light has gone through “It’s a particle.”; “No, it’s a wave.”;
“No, it’s simultaneously both a particle and a wave.”; and finally “It’s
neither a particle nor a wave; it’s something much more mysterious.” This
whole business reminds me of Nargarjuna’s Tetralemma in Buddhist
philosophy. In Western philosophy we think of a statement as being either
true or false. But the Buddhist philosopher Nargarjuna (c. 100 CE) posited
the tetralemma that a statement can be true, or it can be false, or it can be
both true and false at the same time, or it can be neither true nor
false.
Planck at the close of his 1918 Nobel Prize lecture raised a fundamental question:
What becomes of the energy of a photon after complete emission? Does it spread out in all directions with further propagation in the sense of Huygens’ wave theory, so constantly taking up more space, in boundless progressive attenuation? Or does it fly out like a projectile in one direction in the sense of Newton’s emanation theory? In the first case, the quantum would no longer be in the position to concentrate energy upon a single point in space in such a way as to release an electron from its atomic bond, and in the second case, the main triumph of the Maxwell theory—the continuity between the static and the dynamic fields and, with it, the complete understanding we have enjoyed, until now, of the fully investigated interference phenomena—would have to be sacrificed, both being very unhappy consequences for today’s theoreticians.
Be that as it may, in any case no doubt can arise that science will master the dilemma, serious as it is, and that which appears today so unsatisfactory will in fact eventually, seen from a higher vantage point, be distinguished by its special harmony and simplicity. Until this aim is achieved, the problem of the quantum of action will not cease to inspire research and fructify it, and the greater the difficulties which oppose its solution, the more significant it finally will show itself to be for the broadening and deepening of our whole knowledge in physics.
As Planck predicted, science has learned much more about the nature of light and the role it plays in the universe, and the mystery of how photons behave continues to deepen (just Google “photon entanglement”). The word “photon” has itself evolved to mean different things to different people, as reviewed by Kidd et al. (1989). In any case, we still cannot say what light or a photon is in everyday language. We can only describe what it does. This situation is really no different from that of the electron. No one has any idea or model of what an electron “really is,” but that does not prevent electrical engineers from using the known properties of electrons to light our homes and run our computers.
I’ll close this review with two quotes:
All the fifty years of conscious brooding have brought me no closer to the answer to the question: What are light quanta? Of course today every rascal thinks he knows the answer, but he is deluding himself.
—Albert Einstein, quoted in Zajonc (2003)
No one knows what a photon is, and it’s best not to think about it.
—Attributed to Richard Feynman

 See comments posted for this page and leave your own.
See comments posted for this page and leave your own.